Калькулятор систем счисления

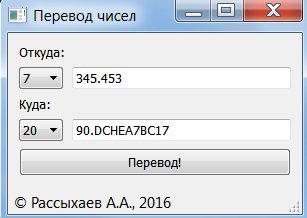
Доступна для скачивания локальная версия программы (win-32bit) перевода чисел в позиционных системах счисления. Программа запускается под платформу Windows XP и выше.

Программа переводит число в десятичную систему, а затем из десятичной - в целевую.

Алгоритм перевода числа в десятичную систему

Рассмотрим на примере перевода двоичного числа 101,11₂

Найдем младшую целую цифру (слева от запятой), сверху отметим ее положение - нулевой разряд. Дробные разряды нумеруются как отрицательные разряды от -1. Основание системы "2" запишем в правом нижнем углу числа. Каждую цифру умножаем на основание исходной системы, возводимое в степень, равную разряду цифры. Складываем полученные числа - это и есть число в десятичной системе.

Алгоритм перевода десятичного числа в любую систему

Переведем число 5,75 обратно в двоичную систему.

1. Сначала отдельно переведем целую часть 5 в двоичную систему. Для этого необходимо делить 5 на 2 (основание целевой системы) до тех пор, пока не получим частное, равное нулю. Полученные остатки запишем в обратной последовательности.

2. Дробную часть 0,75 переведем в двоичную систему, умножая на основание два. При этом после каждого умножения целую часть произведения запишем в дробной части нашего двоичного числа.

Было: 5 = 101₂

0,75 * 2 = 1,5 стало: 101,1₂
убираем целую часть (1)
0,5 * 2 = 1,0 стало: 101,11₂
дробная часть равна нулю, перевод окончен.

Итак, 5,75 = 101,11₂

Не всегда дробную часть десятичного числа возможно перевести в другую систему точно. Попробуйте на досуге перевести число 0,347 в любую другую позиционную систему счисления - алгоритм будет бесконечным (никогда не получим ровно 0 в дробной части).

В компьютерах, использующих двоичную систему, всегда есть погрешности хранения и обработки десятичных дробей. Поэтому вещественные числа в компьютерах хранятся с некоторой точностью (10-16 знаков после запятой). К счастью, такая погрешность во большинстве случаев достаточна.